Проанализируем результат. Рассмотрим частные случаи.

1. Соударения одинаковых шаров (рис. 6.5).

\({m_1} = {m_2}\).

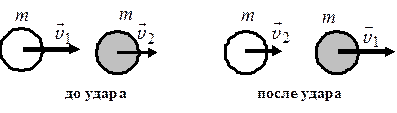
Рис. 6.5

Выражения (6.24) и (6.25) имеют вид

\({u_1} = {v_2},\) \({u_2} = {v_1}\),

т.е. шары равной массы обмениваются скоростями.

2. Один шар до удара покоится:

\({v_2} = 0\).

Выражения (6.24) и (6.25) имеют вид

\({u_1} = \frac{{\left( {{m_1} - {m_2}} \right){\rm{ }}{v_1}}}{{{m_1} + {m_2}}};\quad \;{u_2} = \frac{{2{m_1}{v_1}}}{{{m_1} + {m_2}}}.\) (6.26)

Поведение шаров зависит от соотношения масс:

Поведение шаров зависит от соотношения масс:

а) m₁ > m₂. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (u₁ < \({v_{\rm{1}}}\)), рис. 6.6. Второй шар начинает двигаться в том же направлении;

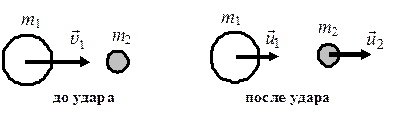
Рис. 6.6

б) m₁<m₂. После удара направление движения первого шара изменится – шар отскакивает обратно (рис. 6.7). Второй шар движется в ту сторону, в которую двигался первый шар до удара.

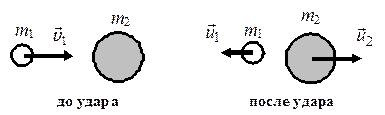
Рис. 6.7

Чем больше разница в массах, тем меньшую энергию передает малый шар большому. При m₁<<m₂u₂= 0. Например, при абсолютно упругом ударе электрона с атомом электрон полностью сохраняет кинетическую энергию;

в) m₁= m₂. После удара остановится первый шар, а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (рис. 6.8).

Рис. 6.8

Таким образом, при абсолютно упругом ударе общая кинетическая энергия тел сохраняется, но распределяется между ними в зависимости от их масс и скоростей.