При рассмотрении закона сохранения энергии материальной точки предполагалось, что материальная точка движется в стационарном силовом поле. Силовое поле, в котором движется материальная частица, возникает благодаря наличию других тел. Чтобы силовое поле было стационарным, не зависящем от времени, тела, создающие это поле, должны быть неподвижны. Таким образом, рассмотренный закон сохранения полной механической энергии относится к случаю: одна материальная точка (тело) движется, а остальные – покоятся.

Сформулируем закон сохранения полной механической энергии в общем случае, когда имеется несколько движущихся материальных точек (тел) – система тел (материальных точек).

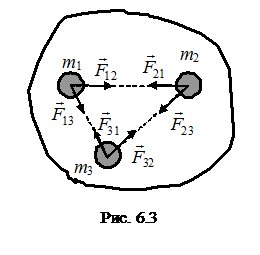
Рассмотрим замкнутую систему из n тел, между которыми действуют только консервативные силы (рис. 6.3).

Под действием этих сил тела внутри системы перемещаются, меняется их скорость и положение, т.е. меняются кинетическая и потенциальная энергии каждого тела и системы в целом.

Запишем второй закон Ньютона для каждого тела:

\(\begin{array}{l}{m_1}\frac{{{\rm{d}}{{\vec v}_1}}}{{{\rm{d}}t}} = {{\vec F}_{12}} + {{\vec F}_{13}} + ... + {{\vec F}_{1n}};\\{m_2}\frac{{{\rm{d}}{{\vec v}_2}}}{{{\rm{d}}t}} = {{\vec F}_{21}} + {{\vec F}_{23}} + ... + {{\vec F}_{2n}};\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\{m_n}\frac{{{\rm{d}}{{\vec v}_n}}}{{{\rm{d}}t}} = {{\vec F}_{n1}} + {{\vec F}_{n2}} + ... + {{\vec F}_{n,n - 1}}.\end{array}\) (6.15)

Под действием сил тела системы совершают перемещения \({\rm{d}}{\vec r_1},{\rm{d}}{\vec r_2},...,{\rm{d}}{\vec r_n}\). Умножим каждое уравнение на соответствующее перемещение. Учитывая, что \({\rm{d}}{\vec r_i} = {\vec v_i}{\rm{d}}t\), получим

\(\begin{array}{l}{m_1}\left( {{{\vec v}_1}{\rm{ d}}{{\vec v}_1}} \right) = ({{\vec F}_{12}} + {{\vec F}_{13}} + ... + {{\vec F}_{1n}}){\rm{d}}{{\vec r}_1};\\{m_2}{\rm{ }}\left( {{{\vec v}_2}{\rm{ }}d{{\vec v}_2}} \right) = \left( {{{\vec F}_{21}} + {{\vec F}_{23}} + ... + {{\vec F}_{2n}}} \right)d{{\vec r}_2};\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\{m_n}{\rm{ }}\left( {{{\vec v}_n}{\rm{ }}d{{\vec v}_n}} \right) = \left( {{{\vec F}_{n1}} + {{\vec F}_{n2}} + ... + {{\vec F}_{n,n - 1}}} \right)d{{\vec r}_n}.\end{array}\)

Сложив эти уравнения, получим

\(\sum\limits_{i = 1}^n {{m_i}\left( {{{\vec v}_i}{\rm{d}}{{\vec v}_i}} \right) - \sum\limits_{i = 1}^n {\left( {{{\vec F}_{i1}} + {{\vec F}_{i2}} + ... + {{\vec F}_{in}}} \right){\rm{d}}{{\vec r}_i} = 0} } \),

или

\(\sum\limits_{i = 1}^n {{\rm{d}}\left( {\frac{{{m_i}v_i^2}}{2}} \right)} - \sum\limits_{i = 1}^n {\left( {{{\vec F}_{i1}} + {{\vec F}_{i2}} + ... + {{\vec F}_{in}}} \right){\rm{d}}{{\vec r}_i} = 0} .\) (6.16)

Первый член левой части равенства

\(\sum\limits_{i = 1}^n {{\rm{d}}\left( {\frac{{{m_i}v_i^2}}{2}} \right)} = {\rm{d}}{E_{к\rm{}}}\), (6.17)

где \({\rm{d}}{E_{к\rm{}}}\) – приращение кинетической энергии системы. Второй член \(\sum\limits_{i = 1}^n {\left( {{{\vec F}_{i1}} + {{\vec F}_{i2}} + ... + {{\vec F}_{in}}} \right)\,} {\rm{d}}{\vec r_i}\) – элементарная работа, совершенная телами системы.

Так как для каждой материальной точки системы \({\rm{d}}{A_i} = - {\rm{d}}{E_{{п\rm{}}i}}\), то \(\sum\limits_{i = 1}^n {{\rm{d}}{A_i} = - \sum\limits_{i = 1}^n {{\rm{d}}{E_{{п\rm{}}i}}} } = - {\rm{d}}{E_{п\rm{}}}\), где \({\rm{d}}{E_{п\rm{}}}\) – приращение потенциальной энергии системы материальных точек, а \({\rm{d}}\left( {{E_{к\rm{}}} + {E_{п\rm{}}}} \right) = 0,\) откуда

\({E_{к\rm{}}} + {E_{п\rm{}}} = {\rm{const}}\). (6.18)

Выражение (6.18) представляет собой закон сохранения механической энергии: полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, сохраняется, т.е. не изменяется со временем. Может происходить лишь превращение кинетической энергии в потенциальную и обратно, причем приращение одной из них в точности равно убыли другой.