Согласно принципу относительности, сформулированному Галилеем в 1636 г., все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы, а законы механики имеют одинаковую математическую форму выражения. В соответствии с этим принципом, никакими механическими опытами, проводимыми в какой-либо инерциальной системе отсчета, нельзя установить, покоится данная система или движется равномерно и прямолинейно.

Классический принцип относительности справедлив для классической механики, при скоростях движения тел, малых по сравнению со скоростью света, т.е. при 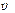<< c.

Преобразования координат Галилея – это формулы преобразования координат материальной точки и времени при переходе от одной инерциальной системы отсчета к другой.

Пусть инерциальная система отсчета К΄движется с постоянной скоростью\({\vec v_{\rm{0}}}\) относительно инерциальной системы отсчета К (рис. 7.1). Преобразования Галилея – это формулы, связывающие между собой координаты x, y, z и x΄, y΄, z΄ материальной точки и время t и t΄ в двух системах отсчета:

\(\vec r = {\vec r_0} + \vec r',\) (7.1)

где \(\vec r - \)радиус-вектор материальной точки в системе К; \(\vec r' - \) – радиус-вектор материальной точки в системе К'; \({\vec r_0}\) – радиус-вектор начала координат системы К' в системе К.

В начальный момент времени (t = 0) начала координат систем К и К' совпадают.

Система К' начинает двигаться относительно К в направлении, совпадающем с вектором \({\vec r_0}\) со скоростью \({\vec v_{\rm{0}}}\):

Рис. 7.1

\({\vec r_0} = {\vec v_0}t\); (7.2)

\(\vec r = {\vec v_{\rm{0}}}t + \vec r'.\) (7.3)

Уравнение (7.3) запишем в проекциях на оси координат:

\(\begin{array}{l}x = {v_{0x}}t + x';\\y = {v_{0y}}t + y';\\z = {v_{0z}}t + z'.\end{array}\) (7.4)

В частном случае, когда К' движется с \({\vec v_{\rm{0}}}\) вдоль положительного направления оси х системы К:

\(\begin{array}{l}x = {v_{0x}}t + x';\\y = y';\\z = z';\\t = t'\end{array}\) (7.5)

– преобразования Галилея.