Длина отрезка – разность координат его начала и конца, измеренных одновременно в выбранной системе отсчёта.

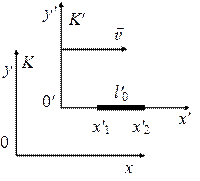
Отрезок (стержень) расположен вдоль оси x' и покоится относительно К' (рис. 7.7).

Его длина в системе К':

\({l'_0} = {x'_2} - {x'_1};\begin{array}{*{20}{c}}{}\end{array}{t'_1} = {t'_2}\). (7.32)

Система К' движется относительно системы К со скоростью .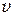

Длина отрезка в системе К

\({l'_0} = \frac{{{x_2} - v{t_2}}}{{\sqrt {1 - {\beta ^2}} }} - \frac{{{x_1} - v{t_1}}}{{\sqrt {1 - {\beta ^2}} }} = \frac{{{x_2} - v{t_2} - {x_1} + v{t_1}}}{{\sqrt {1 - {\beta ^2}} }};\) (7.33)

при\({t_1} = {t_2}\) получаем следующее выражение:

\({l'_0} = \frac{l}{{\sqrt {1 - {\beta ^2}} }}\). (7.34)

Из формулы (7.34) следует, что \(l = {l'_0}\sqrt {1 - {\beta ^2}} ,\) т.е.

\({l'_0} > l.\) (7.35)

Длина стержня \({l'_0}\) в системе, относительно которой он покоится, больше длины стержня l в системе, относительно которой он движется.

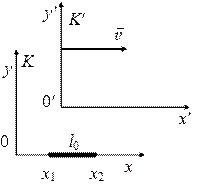
Стержень покоится в системе К, система К' движется относительно К со скоростью \(v\)(рис. 7.8).

В системе К

\({l_0} = {x_2} - {x_1};\quad {t_1} = {t_2}\),

с учетом преобразований

\({l_0} = \frac{{{{x'}_2} - v{{t'}_2} - {{x'}_1} + v{{t'}_1}}}{{\sqrt {1 - {\beta ^2}} }} = \frac{{l'}}{{\sqrt {1 - {\beta ^2}} }}\).

В системе Кʹ

\(l' = {l_0}\sqrt {1 - {\beta ^2}} \quad \Rightarrow \quad {l_0} > l'.\) (7.36)

Длина стержня l₀ в системе, относительно которой он покоится, больше длины стержня l' в системе, относительно которой он движется.

Линейные размеры тела, движущегося относительно инерциальной системы отсчета, уменьшаются в направлении движения в \(\sqrt {1 - {\beta ^2}} \) раз.

Длина отрезка, измеренная в системе отсчёта, в которой он покоится, называется его собственной длиной. Собственная длина всегда имеет наибольшее значение.

Длина отрезка зависит от выбора системы отсчёта, т.е. длина – относительная величина.

В классической механике: \(v < < c\quad \Rightarrow \beta = \frac{v}{c} < < 1\quad \Rightarrow l = {l'_0};\begin{array}{*{20}{c}}{}\end{array}\quad l' = {l_0}.\)