Физика
4. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Преобразования Лоренца
Найдём преобразование для времени.
Из уравнения (7.20) следует, что \(x\sqrt {1 - {\beta ^2}} = x' + vt'\). Подставим полученное выражение в формулу (7.19) и выразим \(t'\). Получаем
\(t' = \frac{{t - x\frac{v}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }}.\) (7.21)
Аналогичные преобразования можно проделать для получения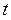 
\(t = \frac{{t' + x'\frac{v}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }}.\) (7.22)
| Прямые преобразования К→К': \(\begin{array}{l}x' = \frac{{x - vt}}{{\sqrt {1 - {\beta ^2}} }};\\y' = y,\quad z' = z;\\t' = \frac{{t - x\frac{v}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }}.\end{array}\) (7.23) | Обратные преобразования К'→ К: \(\begin{array}{l}x = \frac{{x' + vt'}}{{\sqrt {1 - {\beta ^2}} }};\\y = y',\;z = z';\\t = \frac{{t' + x'\frac{v}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }}.\end{array}\) (7.24) |
Классические преобразования Галилея:
| \(\begin{array}{l}x' = x - vt;\\y' = y;\\z' = z;\\t' = t.\end{array}\) | \(\begin{array}{l}x = x' + vt;\\y = y';\\z = z';\\t = t'.\end{array}\) |
При \(v\) << c: \({\left( {\frac{v}{c}} \right)^2} = {\beta ^2} < < 1,\) преобразования Лоренца переходят в преобразования Галилея.
Другие материалы по данной теме
Формула
\(\vec v = {\vec v_0} + \vec v'\)
Определение
Длина отрезка
Видео
"Экспресс-подготовка к ЕГЭ" от МФТИ, Физика, Элементы физики микромира. Элементы СТО