Если система Кʹ движется относительно системы К со скоростью, близкой к скорости света с, то проекции скорости материальной точки на координатные оси в системе К:

\({u_x} = \frac{{{\rm{d}}x}}{{{\rm{d}}t}};\begin{array}{*{20}{c}}{}\end{array}{u_y} = \frac{{{\rm{d}}y}}{{{\rm{d}}t}};\begin{array}{*{20}{c}}{}\end{array}{u_z} = \frac{{{\rm{d}}z}}{{{\rm{d}}t}}.\) (7.39)

Проекции скорости материальной точки на координатные оси в системе К':

\({u'_x} = \frac{{{\rm{d}}x'}}{{{\rm{d}}t'}};\begin{array}{*{20}{c}}{}\end{array}{u'_y} = \frac{{{\rm{d}}y'}}{{{\rm{d}}t'}};\begin{array}{*{20}{c}}{}\end{array}{u'_z} = \frac{{{\rm{d}}z'}}{{{\rm{d}}t'}}.\) (7.40)

Согласно преобразованиям Лоренца:

\(\left. \begin{array}{l}x' = \frac{{x - vt}}{{\sqrt {1 - {\beta ^2}} }};\\y' = y;\\z' = z;\\t' = \frac{{t - x\frac{v}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }},\end{array} \right\}\) \({u'_x} = \frac{{{\rm{d}}x'}}{{{\rm{d}}t'}} = \frac{{{\rm{d}}x - v{\rm{d}}t}}{{{\rm{d}}t - \frac{{v{\rm{d}}x}}{{{c^2}}}}} \cdot \frac{{\sqrt {1 - {\beta ^2}} }}{{\sqrt {1 - {\beta ^2}} }} = \frac{{\frac{{{\rm{d}}x}}{{{\rm{d}}t}} - v}}{{1 - \frac{{v\frac{{{\rm{d}}x}}{{{\rm{d}}t}}}}{{{c^2}}}}} = \frac{{{u_x} - v}}{{1 - \frac{{{u_x}v}}{{{c^2}}}}};\) (7.41)

\({u'_y} = \frac{{{\rm{d}}y'}}{{{\rm{d}}t'}} = \frac{{{\rm{d}}y\sqrt {1 - {\beta ^2}} }}{{{\rm{d}}t - \frac{{v{\rm{d}}x}}{{{c^2}}}}} = \frac{{{u_y}\sqrt {1 - {\beta ^2}} }}{{1 - \frac{{{u_x}v}}{{{c^2}}}}};\) (7.42)

\({u'_z} = \frac{{{\rm{d}}z'}}{{{\rm{d}}t'}} = \frac{{{\rm{d}}z\sqrt {1 - {\beta ^2}} }}{{{\rm{d}}t - \frac{{v{\rm{d}}x}}{{{c^2}}}}} = \frac{{{u_y}\sqrt {1 - {\beta ^2}} }}{{1 - \frac{{{u_x}v}}{{{c^2}}}}};\) (7.43)

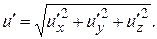 (7.44)

Если материальная точка движется в системе К вдоль оси х со скоростью с:

\(\begin{array}{l}{u_x} = c;\\{{u'}_x} = \frac{{c - v}}{{1 - \frac{{cv}}{{{c^2}}}}} = c,\end{array}\) (7.45)

то её скорость в системе К' равна с. Следовательно, объект, движущийся со скоростью с, будет иметь эту же скорость относительно других систем независимо от того, сколь быстро они движутся (согласие со вторым постулатом Эйнштейна).