Определим эту величину таким же путём, как и в ньютоновской механике. Было доказано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:

\({\rm{d}}{E_{к\rm{}}} = \vec F \cdot {\rm{d}}\vec r = \vec F \cdot \vec v{\rm{d}}t\).

Согласно основному закону релятивистской динамики

\(\vec F{\rm{d}}t = {\rm{d}}\left( {m\vec v} \right) = {\rm{d}}m \cdot \vec v + m{\rm{d}}\vec v\),

где m – релятивистская масса. Поэтому

\({\rm{d}}{E_{к\rm{}}} = {\rm{d}}m\,(\vec v \cdot \vec v{\rm{)}} + m\;{\rm{(d}}\vec v \cdot \vec v{\rm{)}} = {v^2}{\rm{d}}m + m \cdot v{\rm{d}}v\), (7.52)

где учтено, что \(\vec v{\rm{d}}\vec v = v{\rm{d}}v\) и \((\vec v \cdot \vec v{\rm{)}} = {v^{\rm{2}}}\). Эту формулу можно упростить. Для этого формулу зависимости массы от скорости возведём в квадрат и приведём её к виду \({m^2}{c^2} = {m^2}{v^2} + m_0^2{c^2}\).

Найдём дифференциал этого выражения, имея в виду, что m₀ и с – постоянные величины:

2 mc²dm = 2m\(v\)²dm + 2 m²\(v\)d\(v\).

Если теперь разделить это равенство на 2m, то его правая часть совпадёт с выражением для \({\rm{d}}{E_{к\rm{}}}\) (7.52). Отсюда следует,

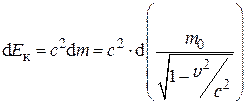. (7.53)

Таким образом, приращение кинетической энергии частицы пропорционально приращению её релятивистской массы.

Кинетическая энергия покоящейся частицы равна нулю, а её масса равна массе покоя m₀. Поэтому, проинтегрировав выражение (7.53), получаем

\({E_{к\rm{}}} = \int {{\rm{d}}{E_{к\rm{}}} = \int\limits_{{m_0}}^m {{c^2}{\rm{d}}m = \left( {m - {m_0}} \right){c^2}} } \), (7.54)

или

\({E_{\rm{}}} = m{c^2} - {m_0}{c^2}\); 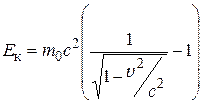. (7.55)

Это и есть выражение для релятивистской кинетической энергии частицы. Как видно, оно сильно отличается от ньютоновского m₀\(v\)²/2. Легко убедиться (пользуясь формулой бинома Ньютона), что при малых скоростях \(v\) << c выражение (7.55) переходит в ньютоновское.