Физика
4. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Преобразования Лоренца
Постулатам Эйнштейна удовлетворяют преобразования Лоренца, предложенные им в 1904 г.
Рассмотрим две инерциальные системы отсчёта K и Kʹ. Пусть
система Kʹ движется относительно системы K со скоростью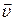 
. Направим координатные оси обеих систем так, как показано на рис. 7.3.
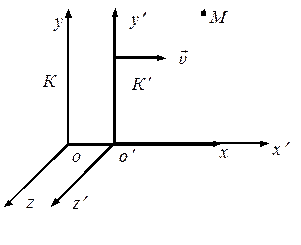
Рис. 7.3
Оси x и xʹ совпадают и направлены параллельно вектору 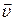. Возьмём за начало отсчёта времени момент, когда начала координат 0 и 0ʹ совпадали.
Пусть в момент времени t¢ в системе K¢ в точке М с координатами x¢, y¢, z¢ произошло некоторое событие, например, вспыхнула лампочка. Требуется найти координаты x, y, z и момент времени t этого события в системе K.
В соответствии с принципом относительности все инерциальные системы отсчета равноправны. В инерциальных системах отсчета физические законы должны иметь одинаковую форму выражения.
|
Рис. 7.4 | Рассмотрим две инерциальные системы отсчета: К и К' (рис. 7.4). К' движется относительно К с \(\vec v\) = const – равномерно и прямолинейно. В начальный момент времени 0 и 0' совпадают. Пусть следим за точкой x' = 0 (начало отсчёта К' ) из системы К, получаем \(x = vt.\) |
Если следим за точкой x = 0 из системы К', то получим следующую зависимость:\(x' = - vt'.\)
Другие материалы по данной теме
Формула
\(\vec v = {\vec v_0} + \vec v'\)
Определение
Длина отрезка
Видео
"Экспресс-подготовка к ЕГЭ" от МФТИ, Физика, Элементы физики микромира. Элементы СТО