Физика
4. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Длительность интервала между событиями
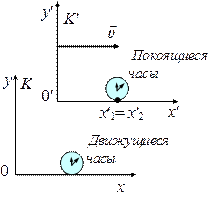
Пусть в системе K' в точке с координатой x'1 произошли два события (рис. 7.5), интервал между событиями в этой системе t'0 = t'2 – t'1, где t'1 – показания часов, когда произошло первое событие, и t'2 – показания часов, когда произошло второе событие. Индекс «0» означает, что событие происходит в одной точке пространства в системе отсчета K'.
|
Рис. 7.5 | Собственное время показывают часы, которые покоятся относительно системы отсчёта в некоторой точке с координатой, в которой произошли 2 события. Эти часы называются покоящимися. Часы, которые движутся относительно системы отсчёта, в некоторой точке которой произошли 2 события, называются движущимися. В системе отсчета \(K'\): \({x'_1} = {x'_2};\begin{array}{*{20}{c}}{}\end{array}{\tau '_0} = {t'_2} - {t'_1}\) (7.27) |
– время между двумя событиями, которые показывают покоящиеся часы.
В системе отсчета К:
\(\tau = {t_2} - {t_1} = \frac{{{{t'}_2} + \frac{{v{{x'}_2}}}{{{c^2}}} - {{t'}_1} - \frac{{v{{x'}_1}}}{{{c^2}}}}}{{\sqrt {1 - {\beta ^2}} }} = \frac{{{{\tau '}_0}}}{{\sqrt {1 - {\beta ^2}} }}\); (7.28)
\(\begin{array}{l}\tau \cdot \sqrt {1 - {\beta ^2}} = {{\tau '}_0};\\\tau > {{\tau '}_0}.\end{array}\) (7.29)
|
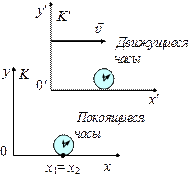
Рис. 7.6 | Движущиеся часы показывают большее время. Часы покоятся в системе К (рис. 7.6). Два события происходят в К в некоторой точке с координатой x1 = x2. В системе Кʹ: \(\tau ' \cdot \sqrt {1 - {\beta ^2}} = {\tau _0}.\) (7.30) \(\underbrace {\tau '}_{{движ\rm{}}{\rm{.ч}}} > \underbrace {{\tau _0}}_{{покоящ\rm{}}{\rm{.ч}}}\) |
Время, измеряемое по часам, движущимся вместе с данным объектом, называется собственным временем этого объекта. Собственное время (жизни объекта) всегда имеет наименьшее значение.
Интервал времени между событиями зависит от выбора системы отсчёта, т.е. время между событиями относительно.
В классической механике:
\(v < < c\quad \Rightarrow \beta = \frac{v}{c} < < 1\quad \Rightarrow \tau ' = {\tau _0};\quad \begin{array}{*{20}{c}}{}\end{array}{\tau '_0} = \tau .\) (7.31)
Другие материалы по данной теме
Видео
"Экспресс-подготовка к ЕГЭ" от МФТИ, Физика, Элементы физики микромира. Элементы СТО
Формула
\(\vec v = {\vec v_0} + \vec v'\)
Определение
Длина отрезка